【python】详细教程：深度相机移动状态下的像素坐标转为世界坐标

作者：朱海生

关键词：python、深度相机、坐标转换

一、前言

深度相机依靠着可以获取距离信息和图像距离的优点被应用在各个领域，本文主要讲解在运动状态下的深度相机的像素中的深度点转化到世界坐标中，此过程使用python代码实现，本文不赘述公式的推理过程，只讲解使用过程。

二、坐标的转化流程

在本文中主要写的是运动中的坐标转换，所以在坐标的转化流程中需要加上刚体变换，在相机的初始状态，我们只有像素和距离信息，在此的基础上我们还需要相机的内参和外参。至于如何获得相机的内参自行查看相机标定。

已知参数：像素坐标、距离信息、相机内参、相机外参

相机外参通常是在外部获得：

首先选择一点作为世界坐标的原点，根据IMU模块获得相机移动的距离和旋转角度，计算相机外参代码如下：

import cv2
import numpy as np

# 获得旋转矩阵（从旋转向量转换）
def pose_matrix():
    # 旋转向量（单位：弧度），实际应从传感器获取
    # 注意：变量名修正，非余弦值，而是旋转向量的三个分量
    rot_vec_x = 0.0
    rot_vec_y = 0.0
    rot_vec_z = 0.0  # 示例：零旋转向量（对应单位矩阵）
    
    # 旋转向量格式：(x, y, z)，使用Rodrigues公式转换为3x3旋转矩阵
    rot_vec = np.array([rot_vec_x, rot_vec_y, rot_vec_z], dtype=np.float32)
    rot_matrix, _ = cv2.Rodrigues(rot_vec)  # 返回(旋转矩阵, 雅可比矩阵)
    
    print("旋转矩阵:\n", rot_matrix)
    return rot_matrix

# 获得平移向量（修正为标准3x1向量格式）
def translate_matrix():
    # 平移参数（单位：通常为米/毫米，根据传感器定义）
    trans_x = 0.0
    trans_y = 0.0
    trans_z = 0.0  # 示例：零平移
    
    # 平移向量应为3x1列向量（符合相机模型规范）
    # 修正：移除错误的3x3对角矩阵，改为标准平移向量
    trans_vec = np.array([[trans_x], [trans_y], [trans_z]], dtype=np.float32)
    
    return trans_vec

# 测试
if __name__ == "__main__":
    # 测试旋转矩阵（零旋转应为单位矩阵）
    rot = pose_matrix()
    # 测试平移向量（零平移应为全零3x1向量）
    trans = translate_matrix()
    print("平移向量:\n", trans)

三、计算公式及参数讲解

相机的像素坐标转为世界坐标公式如下：

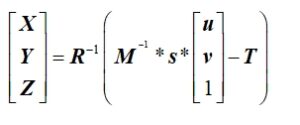
（X、Y、Z）为世界坐标，R为上述的旋转矩阵，T为上述的平移矩阵，M为相机的内参，通过相机标定获取，s为尺度因子。

尺度因子的计算如下：

上述的Zw为深度相机测出的距离。

四、python代码

Python的完全版代码如下：

import cv2
import numpy as np
import math
import path  # 确保已安装path库（若使用需导入）

# 获得旋转矩阵（使用Rodrigues公式从旋转向量转换）
def pose_matrix():
    # 旋转向量（单位：弧度），实际应从传感器获取
    x_cos, y_cos, z_cos = 0, 0, 0  # 示例值：无旋转
    rot_vec = np.array([x_cos, y_cos, z_cos], dtype=np.float32)
    # Rodrigues转换：旋转向量→旋转矩阵（3x3）
    rot_matrix, _ = cv2.Rodrigues(rot_vec)
    return rot_matrix

# 获得平移矩阵（3x1向量，实际应从传感器获取）
def translate_matrix():
    x, y, z = 0, 0, 0  # 示例平移量
    return np.array([[x], [y], [z]], dtype=np.float32)  # 修正为3x1向量（标准平移向量格式）

# 相机内参矩阵（3x3）
def internal_reference():
    # 示例内参：fx, fy为焦距；cx, cy为主点坐标
    return np.array([
        [557.34692705, 0, 320.15921429],
        [0, 574.29121785, 233.20683435],
        [0, 0, 1]
    ], dtype=np.float32)

# 像素坐标转为齐次坐标矩阵（3x1）
def pixel_coordinate_matrix(pixel_coordinate):
    u, v = pixel_coordinate  # (u, v)为像素坐标
    return np.array([[u], [v], [1]], dtype=np.float32)  # 齐次坐标：[u, v, 1]^T

# 像素坐标转世界坐标（核心函数）
def pixel2world(pixel_coordinate, s):
    # 1. 获取基础矩阵
    rot_matrix = pose_matrix()  # 旋转矩阵（3x3）
    trans_matrix = translate_matrix()  # 平移向量（3x1）
    pixel_matrix = pixel_coordinate_matrix(pixel_coordinate)  # 像素齐次坐标（3x1）
    internal_matrix = internal_reference()  # 内参矩阵（3x3）
    
    # 2. 计算关键矩阵（修正：内参需求逆，而非转置）
    inv_internal = np.linalg.inv(internal_matrix)  # 内参逆矩阵（核心修正）
    
    # 3. 计算相机坐标系下的坐标（齐次）
    cam_homogeneous = s * np.dot(inv_internal, pixel_matrix)  # [Xc, Yc, Zc, s]^T（齐次）
    cam_coords = cam_homogeneous[:3]  # 相机坐标系坐标（3x1）：[Xc, Yc, Zc]^T
    
    # 4. 转换到世界坐标系（世界 = R^T * (相机 - 平移)）
    world_coords = np.dot(rot_matrix.T, (cam_coords - trans_matrix))  # 核心公式
    
    return world_coords

# 测试：像素坐标(200, 500)，尺度参数s=300
world = pixel2world((200, 500), 300)
print("世界坐标：\n", world)

五、总结

上述代码可完成将深度相机中的像素坐标转为世界坐标，通过此方法可是实现深度相机的3维建模。